平面図形問題の魅力と問題作りへのこだわり。『究極の平面図形＜相似・面積比＞』開発者インタビュー<後編>

子どもたちに考えることの楽しさを感じてもらうには、「面白い問題」が不可欠です。ただ簡単なだけ、難しいだけの作業をこなすような問題ではなく、「面白い問題」を作るためには、何が必要なのでしょうか。

後編となる今回の記事では、アプリ教材『究極の平面図形＜相似・面積比＞』について、子どもたちの反応と、問題作成における工夫や相似問題の魅力について、問題の作成を担当したコンテンツクリエイターの声をお届けします。

前編ではアプリ教材『究極の平面図形＜相似・面積比＞』の特徴と、子ども目線に寄り添ったUI・UX設計について取り上げています。ぜひ合わせてご覧ください。

相似が「見える」感覚を体験できるアプリ教材『究極の平面図形＜相似・面積比＞』開発者インタビュー<前編>　

『究極の平面図形＜相似・面積比＞』公式HP：https://similarity.ultimate-math.com/

子どもたちの反応から見えてきたこと

──実際に子どもたちに教材を使ってみてもらって、どのように感じましたか？

山本：子どもたちが問題にじっくり取り組んでくれていたのがとても印象的でした。特に、幅広い難易度の問題を用意したことで、得意な子でも十分にやりごたえを感じてもらえたようです。

──問題の難易度設定にはどのような工夫がありましたか？

山本：100問という量がある中で、難易度がのっぺりしていると子どもたちも飽きてしまいます。そこで問題集として、簡単なものから難しいものまでバラエティを持たせました。また、1問1問なるべく違いを出すことも意識しています。

子どもたちに楽しんでもらえる「きれいな問題」を作りたい

 ──問題作成において特に意識されていたポイントはありますか？

山本：なるべく”きれいな問題”を作りたいという意識がありました。例えば、隣り合っている辺の比を求めるというような、自然な設定を意識しています。また、少ない情報を駆使してそれだけで解けるような問題は美しいと思います。

──解き方についてはどのような配慮がありましたか？

山本：自然な解き方になるべく対応できるように心がけています。自然な解き方とは、『ここを求めたい』『そのためにはここがわかっていないといけない』という風に考えていくことでたどり着く解き方だと考えています。

技を適用する場所を選択肢から選ぶという形式なので、解き方をある程度絞らざるを得ない面はありますが、できるだけ子どもたちの自然な思考の流れを阻害したくないと考えています。

例えば、技を使う順番については、自然な解き方だと思われる範囲でなるべく自由な順番で解けるようにしています。

この問題では、3つの技を使いますが、技を使う順番は3パターンあります。

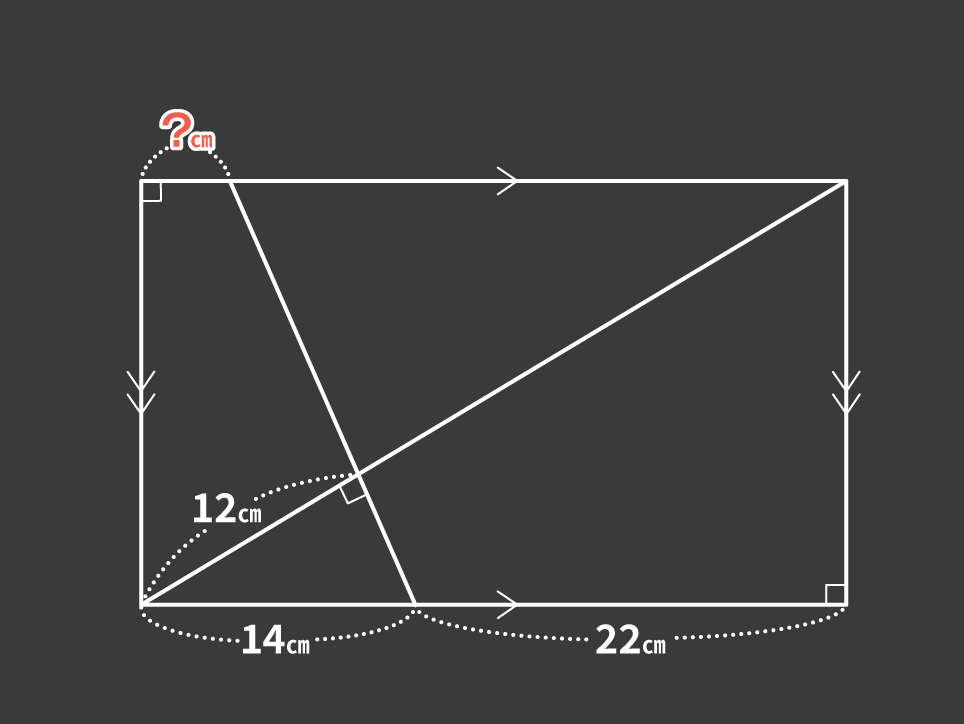
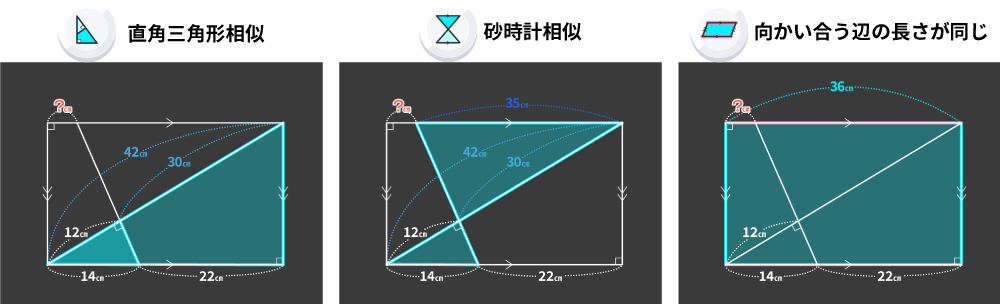
「直角三角形の相似でわかったことを使って、砂時計相似でさらに別の値を求める」という順番は必須ですが、「向かい合う辺の長さが同じ」という技はいつ使っても問題ありません。『究極の平面図形＜相似・面積比＞』では、3パターンのどの順番でも解くことができるようにしています。

平面図形問題の面白さと難しさ

──平面図形の問題の魅力を教えてください。

山本：平面図形の問題の面白さは、わかっていることを使って、わからなかったことを順番に導き出していく過程にあると思っています。例えば、パズル作家の稲葉直貴さんの「面積迷路」で味わえるような面白さですね。

※「面積迷路」はパズル作家の稲葉直貴さんが考案したパズルで、書籍やゲーム等、様々な媒体で展開されています。

『究極の平面図形＜相似・面積比＞』は教材ではあるけれど、パズル的な楽しさを感じられるようにしたいと思って問題を作成しました。

──作成した問題で、お気に入りのものを教えてください。

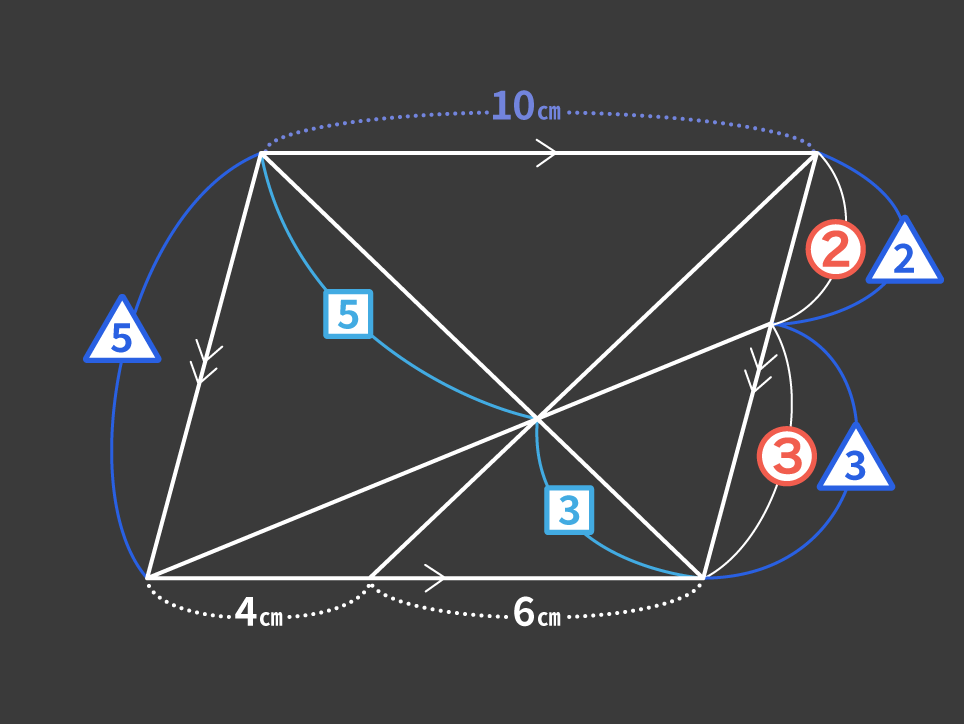
『究極の平面図形＜相似・面積比＞』でお気に入りの問題は次の問題です。

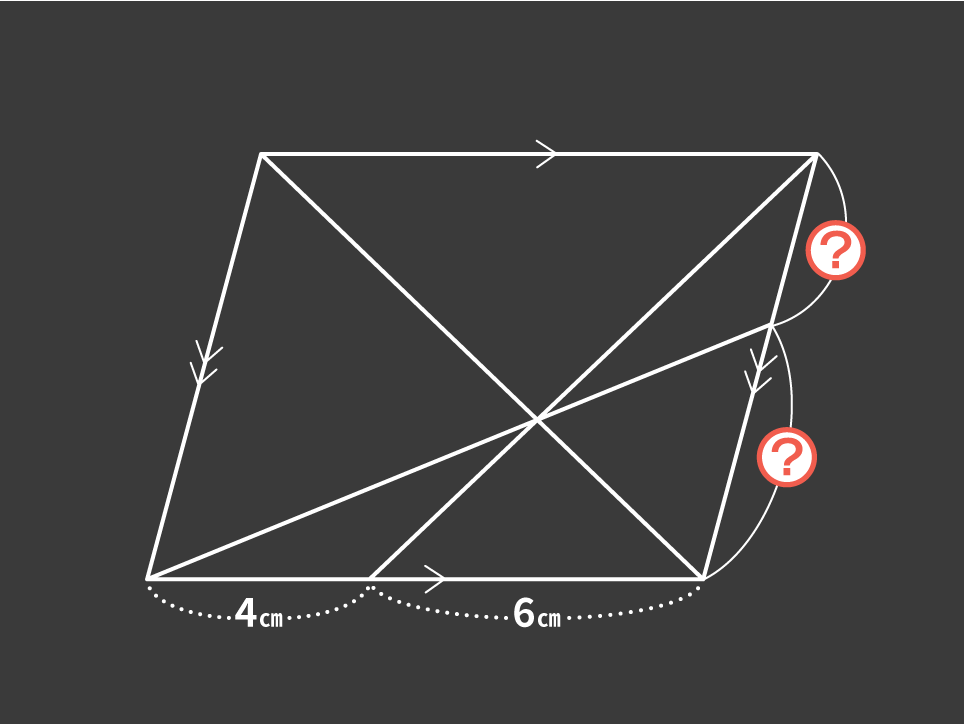
平行四辺形の中に3本の線を引いた図形で、明かされている値は下の辺の長さのみなのに、相似と平行四辺形の性質を駆使することで、斜めの辺の比が明かされていくというちょっとした意外性を味わえる問題です。先ほど述べた、「少ない情報を駆使してそれだけで解けるような問題」になっていると思います。

編集後記

ワンダーファイの教材開発では、子どもたちが自ら考えることの楽しさを感じられるような工夫を常に模索しています。平面図形の問題の「わかっていることを使って、未知の部分を明らかにしていく」という過程には、探求心を刺激する魅力があります。

問題を解くことは、単なる正解の特定ではなく、思考のプロセスを楽しむ旅でもあります。弊社はこれからも、子どもたちが「わかった！」という喜びを感じられる教材づくりに取り組んでまいります。